Vortex tube

A vortex tube takes in high-pressure air at 650 kPa and 305 K, and splits it into two streams at a lower pressure, 100 kPa: one at a higher temperature of 325 K and one at a lower temperature. The fraction of mass entering that leaves at the cold outlet is $f=0.25$. The vortex tube operates continuously at steady state, is adiabatic, and performs/experiences no work. Air should be modeled as an ideal gas with constant specific heat: $R=287$ J/kg⋅K and $c_p=1004$ J/kg⋅K.

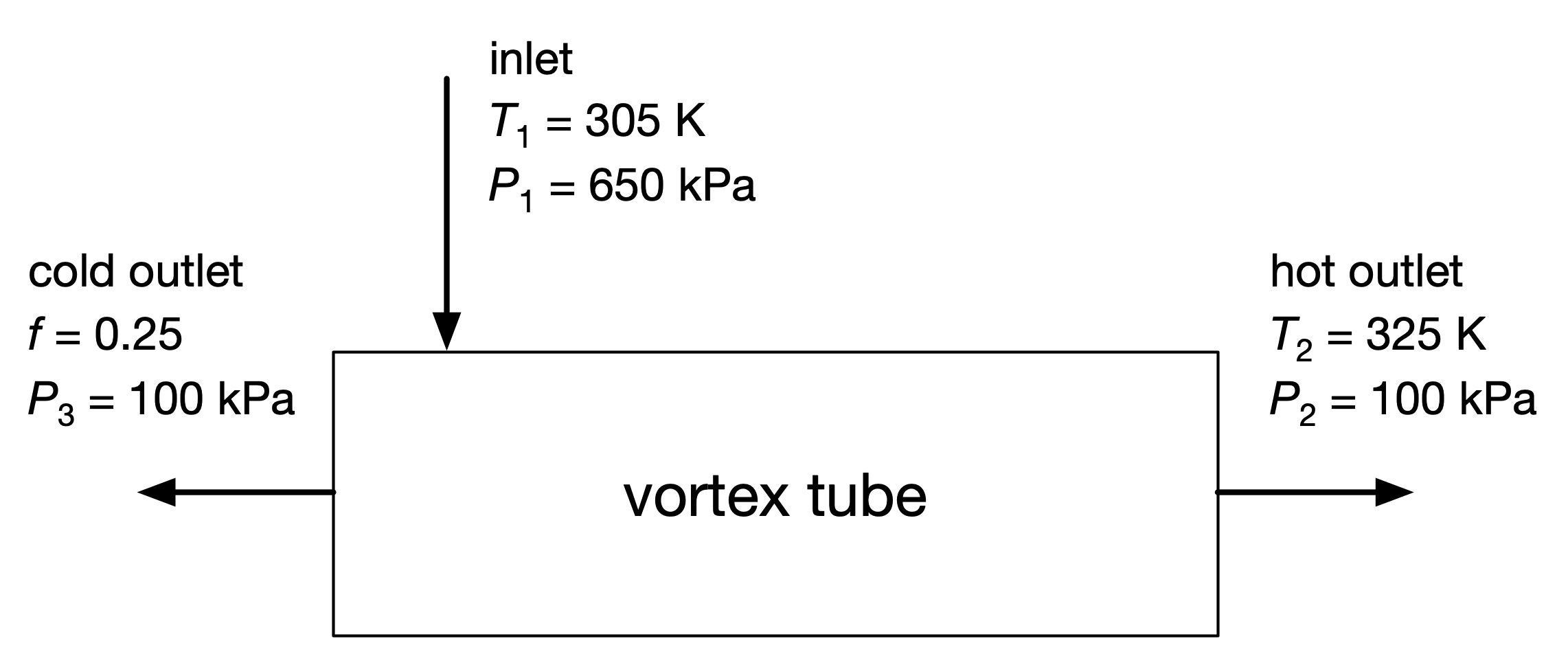
Problem: Determine the temperature at the cold end. Then, determine whether this device is physically possible.

# Enter the known quantities
import numpy as np
from pint import UnitRegistry
ureg = UnitRegistry()
Q_ = ureg.Quantity

gas_constant = Q_(287, 'J/(kg K)')
cp = Q_(1004, 'J/(kg K)')

temp_1 = Q_(305, 'K')
pres_1 = Q_(650, 'kPa')

temp_2 = Q_(325, 'K')
pres_2 = Q_(100, 'kPa')

f = 0.25
pres_3 = Q_(100, 'kPa')

First, we can find the temperature at the cold outlet by performing an energy balance on the device:

$$\begin{array}{r}{\dot{m}}_1{u}_1={\dot{m}}_3{u}_3+{\dot{m}}_2{u}_2\\ \dot{m}{c}_p{T}_1=f\dot{m}{c}_p{T}_3+(1-f)\dot{m}{c}_p{T}_2\\ T_3=\frac{T_1-(1-f)T_2}{f}\end{array}$$

temp_3 = (temp_1 - (1-f)*temp_2) / f
print(f'Temperature at cold outlet: {temp_3: .2f}')

Temperature at cold outlet: 245.00 kelvin

Now, examine whether the device is physically possible by performing an entropy balance:

$$\begin{array}{r}\dot{m}{s}_1+{\dot{S}}_{\text{gen}}=f\dot{m}{s}_3+(1-f)\dot{m}{s}_2\\ \frac{{\dot{S}}_{\text{gen}}}{\dot{m}}=f{s}_3+(1-f)s_2=f(s_3-s_2)+(s_2-s_1).\end{array}$$

We can obtain the $\mathrm{\Delta }s$ values by using the relationship for an ideal gas with constant specific heat:

(19)$$\mathrm{\Delta }{s}_{1-2}=c_p\ln \left(\frac{T_2}{T_1}\right)-R\ln \left(\frac{p_2}{p_1}\right)$$

delta_s_12 = (
    cp * np.log(temp_2/temp_1) - 
    gas_constant * np.log(pres_2/pres_1)
    )
delta_s_23 = (
    cp * np.log(temp_3/temp_2) - 
    gas_constant * np.log(pres_3/pres_2)
    )

entropy_gen = f * delta_s_23 + delta_s_12
print(f'Entropy generation rate: {entropy_gen: .2f}')

Entropy generation rate: 530.05 joule / kelvin / kilogram

Since the rate of entropy generation is positive, this device can operate as described.