Adiabatic flame temperature#

Consider a stoichiometric mixture of ethane (C\(_2\)H\(_6\)) and air at 25°C and 1 atm. Calculate the adiabatic flame temperature, assuming complete combustion.

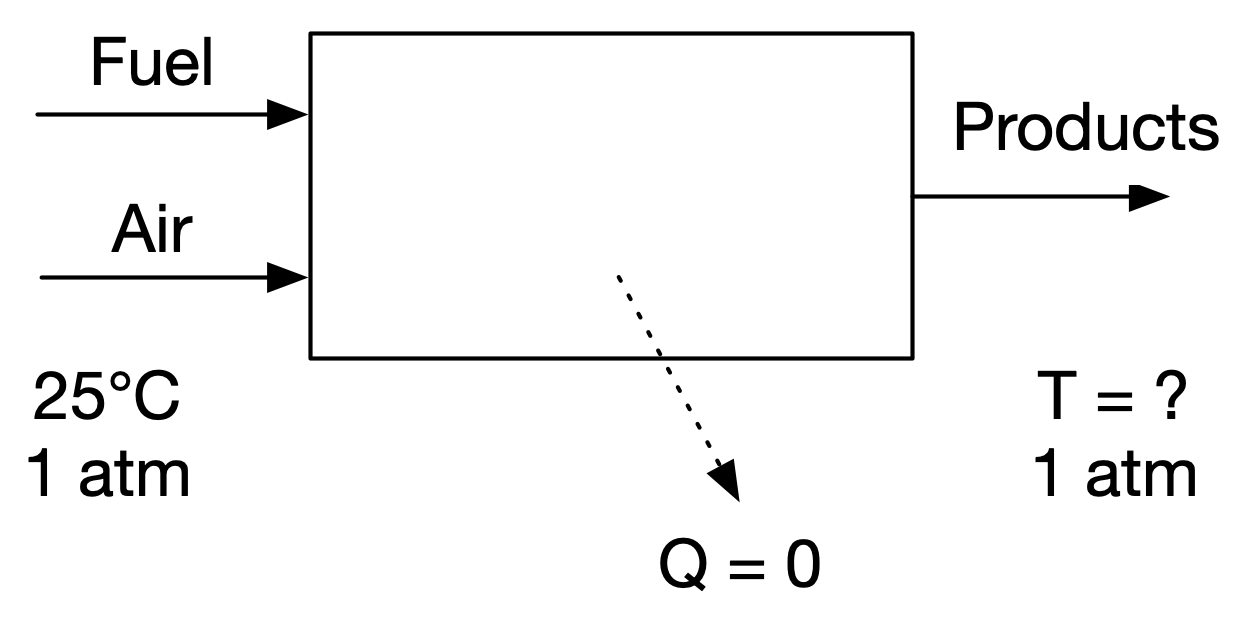
Control volume for adiabatic flame temperature

We can find the adiabatic flame temperature by performing a steady-state energy balance on this system:

(36)#\[\begin{equation} H_{\text{reactants}} = Q_{\text{out}} + H_{\text{products}} \end{equation}\]

where \(H\) is the total enthalpy and \(Q_{\text{out}} = 0\) is the (zero) heat release.

First, we need to determine the composition of the products.

import numpy as np
import cantera as ct
from scipy.optimize import root_scalar

from pint import UnitRegistry
ureg = UnitRegistry()
Q_ = ureg.Quantity

# for convenience:
def to_si(quant):
    '''Converts a Pint Quantity to magnitude at base SI units.
    '''
    return quant.to_base_units().magnitude

The combustion reaction is

(37)#\[\begin{equation} \text{C}_2 \text{H}_6 + a (0.21 \text{O}_2 + 0.79 \text{N}_2) \rightarrow b \text{CO}_2 + c \text{H}_2 \text{O} + d \text{N}_2 \end{equation}\]

and we can solve for the stoichiometric coefficients \(a\), \(b\), \(c\), and \(d\) by performing elemental balances:

b = 2.0
c = 6.0 / 2.0
a = (2*b + c) / (2*0.21)
d = (a*0.79*2) / 2.0
print(f'a={a: .3f}, b={b: .2f}, c={c: .2f}, d={d: .3f}')

a= 16.667, b= 2.00, c= 3.00, d= 13.167

So the stoichiometric reaction is

(38)#\[\begin{equation} \text{C}_2 \text{H}_6 + 16.667 (0.21 \text{O}_2 + 0.79 \text{N}_2) \rightarrow 2 \text{CO}_2 + 3 \text{H}_2 \text{O} + 13.167 \text{N}_2 \end{equation}\]

We can then use these stoichiometric coefficients in our energy balance:

\[ \begin{aligned} \sum_{i=1}^{N_R} n_i \overline{h}_{i} ( T_{\text{in}}, P) = \sum_{i=1}^{N_P} n_i \overline{h}_{i} (T_{\text{out}}, P) \end{aligned} \]

where \(N_R\) and \(N_P\) are the numbers of reactants and products, \(T_{\text{in}}\) is the inlet temperature, \(P\) is the pressure, \(\overline{h}_{i}\) is the standard molar enthalpy of a particular species \(i\), and \(T_{\text{out}}\) is the unknown final temperature.

We can find that temperature by setting this up as a root-finding problem to find temperature.

pressure = Q_(1, 'atm')
temperature_in = Q_(25, 'degC')

# calculate inlet enthalpies for each species
gas = ct.Solution('gri30.cti')
gas.TPX = to_si(temperature_in), to_si(pressure), 'C2H6:1.0'
enthalpy_c2h6 = gas.enthalpy_mole

gas.TPX = to_si(temperature_in), to_si(pressure), 'N2:1.0'
enthalpy_n2 = gas.enthalpy_mole

gas.TPX = to_si(temperature_in), to_si(pressure), 'O2:1.0'
enthalpy_o2 = gas.enthalpy_mole

enthalpy_reactants = (
    enthalpy_c2h6 + a * (0.21 * enthalpy_o2 + 0.79 * enthalpy_n2)
    )

/tmp/ipykernel_4536/2060177122.py:5: DeprecationWarning: XML_Node::build: 
The CTI and XML input file formats are deprecated and will be removed in
Cantera 3.0. Use 'cti2yaml.py' or 'ctml2yaml.py' to convert CTI or XML input
files to the YAML format. See https://cantera.org/tutorials/legacy2yaml.html
for more information.
  gas = ct.Solution('gri30.cti')

def get_flame_temp(temp, pressure, enthalpy_reactants, gas):    
    gas.TPX = temp, pressure, 'CO2:1.0'
    enthalpy_co2 = gas.enthalpy_mole
    
    gas.TPX = temp, pressure, 'H2O:1.0'
    enthalpy_h2o = gas.enthalpy_mole
    
    gas.TPX = temp, pressure, 'N2:1.0'
    enthalpy_n2 = gas.enthalpy_mole
    
    return (
        2.0*enthalpy_co2 + 3.0*enthalpy_h2o + 13.167*enthalpy_n2 - 
        enthalpy_reactants
        )
    
gas = ct.Solution('gri30.cti')

sol = root_scalar(
    get_flame_temp,
    x0=1000., x1=2000.,
    args=(to_si(pressure), enthalpy_reactants, gas)
    )

print(f'Adiabatic flame temperature: {sol.root: .2f} K')

Adiabatic flame temperature:  2379.21 K

Solve using mixtures#

We can also solve this problem by representing the reactants and products as mixtures, using the Solution class and giving the numbers of moles as input for mole fractions, X. (These will be automatically normalized to sum to 1.0).

The molar enthalpies of the reactants and products are then just the molar enthalpies of the mixtures.

One catch: to ensure the results match, we need to ensure that we multiply the molar enthalpy of each mixture by the number of moles of each, since total enthalpy is conserved rather than specific enthalpy.

gas = ct.Solution('gri30.cti')
gas.TPX = (
    to_si(temperature_in), to_si(pressure),
    'C2H6:1.0, O2:3.5, N2:13.167'
    )

# Multiply the mixture specific enthalpy by 
# the total number of moles.
total_moles = 1.0 + 3.5 + 13.167
enthalpy_reactants = gas.enthalpy_mole * total_moles

def get_flame_temp(temp, pressure, enthalpy_in, gas):
    gas.TPX = (
        temp, pressure, 
        'CO2:2.0, H2O:3.0, N2:13.167'
        )
    # Multiply the mixture specific enthalpy by 
    # the total number of moles.
    total_moles = 2.0 + 3.0 + 13.167
    enthalpy_products = gas.enthalpy_mole * total_moles
        
    return (enthalpy_products - enthalpy_in)
    
gas = ct.Solution('gri30.cti')

sol = root_scalar(
    get_flame_temp,
    x0=1000., x1=2000.,
    args=(to_si(pressure), enthalpy_reactants, gas)
    )

print(f'Adiabatic flame temperature: {sol.root: .2f} K')

Adiabatic flame temperature:  2379.21 K

As expected, we get the same solution using this approach, but with significantly less coding effort.

Compare to Cantera solution#

Lastly, we can also find the adiabatic flame temperature by using the built-in equilibrate() method provided by the Solution class.

Given an initial state, this finds the equilibrium state (composition and temperature) while holding two properties constant. For the adiabatic flame temperature, we hold enthalpy and pressure constant (equilibrate('HP')).

To ensure that only the species involved in stoichiometric, complete combustion are considered, we also need to construct a new mixture object that only contains the fuel, oxygen, nitrogen, carbon dioxide, and water.

# Get all of the Species objects defined in the GRI 3.0 mechanism
species = {S.name: S for S in ct.Species.listFromFile('gri30.cti')}

# Create an IdealGas object with species representing complete combustion
complete_species = [species[S] for S in ('C2H6','O2','CO2','H2O','N2')]
gas = ct.Solution(thermo='IdealGas', species=complete_species)

gas.TP = to_si(temperature_in), to_si(pressure)
gas.set_equivalence_ratio(1.0, 'C2H6', 'O2:1, N2:3.76')
gas.equilibrate('HP')


# for comparing to the other solutions
num_moles = 2.0 + 3.0 + 13.167

print(f'Adiabatic flame temperature: {gas.T: .2f} K')

print('Moles of species at equilibrium:')
for sp, mole_fraction in zip(gas.species_names, gas.X):
    print(f'{sp:4}  {mole_fraction*num_moles: 5.3e}')

Adiabatic flame temperature:  2379.85 K
Moles of species at equilibrium:
C2H6   2.304e-08
O2     8.065e-08
CO2    2.001e+00
H2O    3.001e+00
N2     1.317e+01

/tmp/ipykernel_4536/2098430063.py:2: DeprecationWarning: Static method 'listFromFile' is renamed to 'list_from_file'. The old name will be removed after Cantera 2.6.
  species = {S.name: S for S in ct.Species.listFromFile('gri30.cti')}

This result is extremely close to what we obtained previously; the temperature is slightly different due to the (very) small amounts of reactants still present at equilibrium.