Sample Quiz 3 problems: BVPs

Problem 1: Finite difference method

The temperature distribution \(T(r)\) in an annular fin of inner radius \(r_1\) and outer radius \(r_2\) is described by the equation

(24)\[\begin{equation} r \frac{d^2 T}{dr^2} + \frac{dT}{dr} - rm^2 (T - T_{\infty}) = 0 \;, \end{equation}\]

where \(r\) is the radial distance from the centerline (the independent variable) and \(m^2\) is a constant that depends on the heat transfer coefficient, thermal conductivity, and thickness of the annulus. Assuming we choose a spatial step size \(\Delta r\),

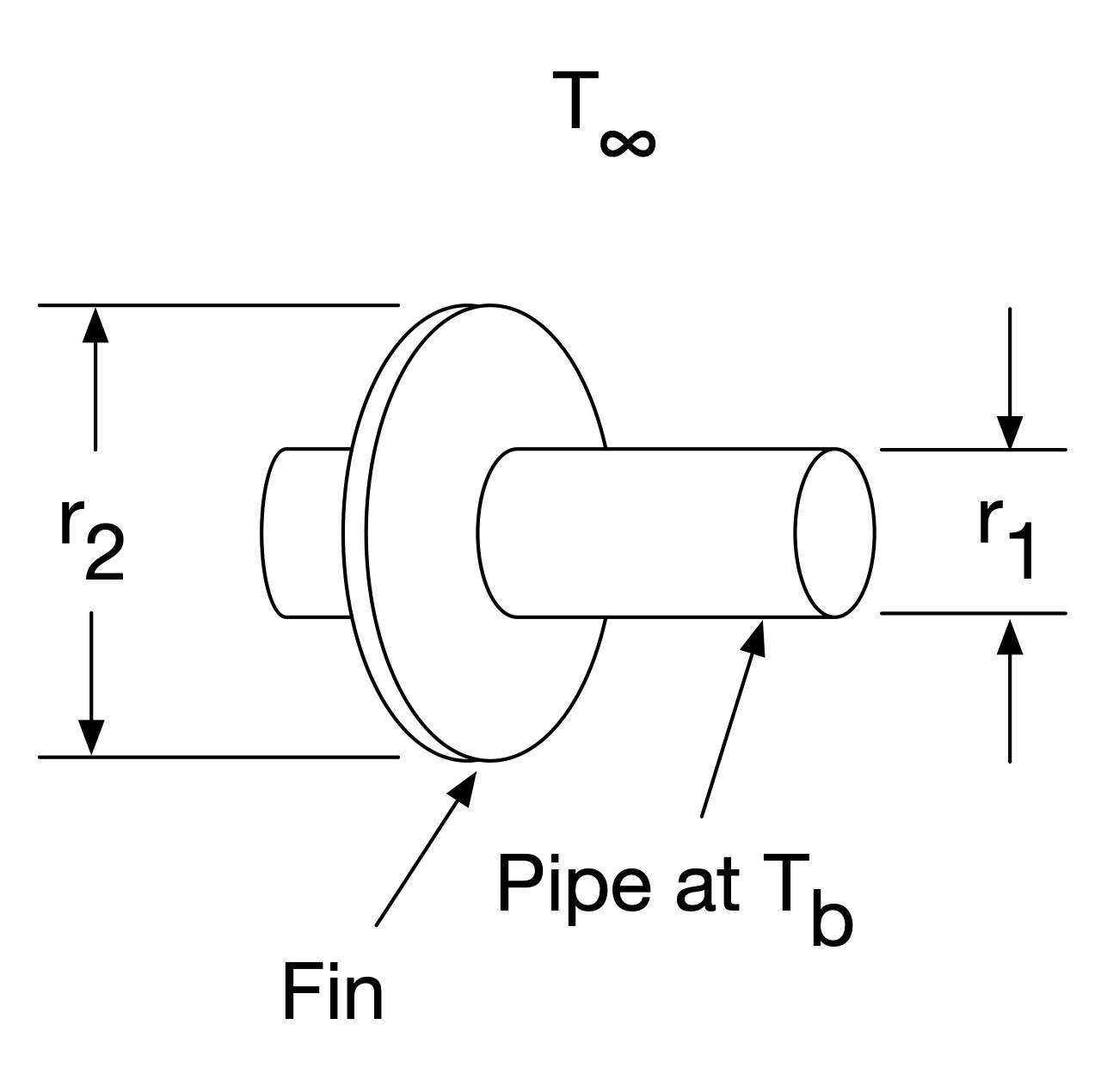
Fig. 1 Annular fin

a.) Write the finite-difference representation of the ODE (that applies at a location \(r_i\)), using central differences.

b.) Based on the last part, write the recursion formula.

c.) The boundary condition at the outer radius \(r = r_2\) is described by convection heat transfer:

(25)\[\begin{equation} -k \left. \frac{dT}{dr} \right|_{r=r_2} = h \left[ T(r=r_2) - T_{\infty} \right] \;. \end{equation}\]

Write the boundary condition at \(r = r_2\) in recursion form (i.e., the equation you would implement into your system of equations to solve for temperature).

Solution

a.) Replace the derivatives in the given ODE with finite differences, and replace any locations with the \(i\) location:

(26)\[\begin{equation} r_i \frac{T_{i-1} - 2T_i + T_{i+1}}{\Delta r^2} + \frac{T_{i+1} - T_{i-1}}{2\Delta r} - r_i m^2 (T_i - T_{\infty}) = 0 \end{equation}\]

or

(27)\[\begin{equation} r_i (T_{i-1} - 2T_i + T_{i+1}) + \frac{\Delta r}{2} (T_{i+1} - T_{i-1}) - r_i m^2 \Delta r^2 (T_i - T_{\infty}) = 0 \end{equation}\]

b.) Rearrange and combine terms:

(28)\[\begin{align} r_i (T_{i-1} - 2T_i + T_{i+1}) + \frac{\Delta r}{2} (T_{i+1} - T_{i-1}) - r_i m^2 \Delta r^2 (T_i - T_{\infty}) &= 0 \\ r_i (T_{i-1} - 2T_i + T_{i+1}) + \frac{\Delta r}{2} (T_{i+1} - T_{i-1}) - r_i m^2 \Delta r^2 T_i &= -r_i m^2 \Delta r^2 T_{\infty} \\ \left(r_i - \frac{\Delta r}{2}\right) T_{i-1} + \left( -2 r_i - r_i m^2 \Delta r^2 \right) T_i + \left( r_i + \frac{\Delta r}{2} \right) T_{i+1} &= -r_i m^2 \Delta r^2 T_{\infty} \end{align}\]

c.) We can use a backward difference to approximate the \(dT/dr\) term. \(T_n\) represents the temperature at node \(n\) where \(r_n = r_2\):

(29)\[\begin{align} -k \frac{T_n - T_{n-1}}{\Delta r} &= h (T_n - T_{\infty}) \\ -k (T_n - T_{n-1}) &= h \Delta r (T_n - T_{\infty}) \\ k T_{n-1} - (k + h\Delta r) T_n &= -h \Delta r T_{\infty} \end{align}\]

Problem 2: eigenvalue

Given the equation \(y^{\prime\prime} + 9 \lambda^2 y = 0\) with \(y(0) = 0\) and \(y(2) = 0\),

a.) Find the expression that gives all eigenvalues (\(\lambda\)). What is the eigenfunction?

b.) Calculate the principal eigenvalue.

Solution

a.)

(30)\[\begin{gather} y(x) = A \sin (3 \lambda x) + B \cos (3 \lambda x) \\ \text{Apply BCs: } y(x=0) = 0 = A \sin(0) + B \cos(0) = B \\ \therefore B = 0 \\ y(x) = A \sin (3 \lambda x) \\ y(x=2) = 0 = A \sin (3 \lambda 2) \\ A \neq 0 \text{ so } \sin(3 \lambda 2) = \sin(6 \lambda) = 0 \therefore 6 \lambda = n \pi \quad n=1,2,3,\ldots \\ \lambda = \frac{n \pi}{6} \quad n=1,2,3,\ldots,\infty \end{gather}\]

The eigenfunction is then the solution function associated with an eigenvalue:

(31)\[\begin{equation} y_n = A_n \sin \left( \frac{n \pi x}{2} \right) \quad n = 1, 2, 3, \ldots, \infty \end{equation}\]

b.) The principal eigenvalue is just that associated with \(n = 1\):

(32)\[\begin{equation} \lambda_p = \lambda_1 = \frac{\pi}{6} \end{equation}\]

Problem 3: shooting method

Use the shooting method to solve the boundary value problem

(33)\[\begin{equation} y^{\prime\prime} - 4y = 0 \end{equation}\]

where \(y(0) = 0\) and \(y(1) = 3\). Find the initial value of \(y'\) (meaning, \(y'(0)\)) that satisfies the given boundary conditions. Use the forward Euler method with a step size of \(\Delta x = 0.5\).

Solution

First decompose into two 1st-order ODEs:

(34)\[\begin{align} z_1' &= y' = z_2 \\ z_2' &= y'' = 4 z_1 \end{align}\]

with BCs \(z_1 (x=0) = z_{1,1} = 0\) and \(z_1(x=1) = z_{1,3} = 3\), we do not know \(y'(0) = z_2(x=0) = z_{2,1} = ?\)

Try some guess #1: \(y' (0) = 0 = z_2 (0)\), with the forward Euler method:

(35)\[\begin{align} z_{1,2} = z_1 (0.5) &= z_1 (0) + z_2(0) 0.5 = 0 \\ z_{2,2} = z_2 (0.5) &= z_2 (0) + \left( 4z_1(0) \right) 0.5 = 0 \\ z_{1,3} = z_1 (1.0) &= z_1 (0.5) + z_2(0.5) 0.5 = 0 \leftarrow \text{solution 1} \\ z_{2,3} = z_2 (1.0) &= z_2 (0.5) + \left( 4z_1(0.5) \right) 0.5 = 0 \end{align}\]

so for solution 1: \(y(1) = 0 \neq 3\).

For guess #2: \(y' (0) = 2 = z_2 (0)\), with the forward Euler method:

(36)\[\begin{align} z_1 (0.5) &= z_1 (0) + z_2(0) 0.5 = 1.0 \\ z_2 (0.5) &= z_2 (0) + \left( 4z_1(0) \right) 0.5 = 2.0 \\ z_1 (1.0) &= z_1 (0.5) + z_2(0.5) 0.5 = 2.0 \leftarrow \text{solution 2} \\ z_2 (1.0) &= z_2 (0.5) + \left( 4z_1(0.5) \right) 0.5 = 4.0 \end{align}\]

so for solution 1: \(y(1) = 2 \neq 3\).

For guess #3, we can interpolate:

(37)\[\begin{align} m &= \frac{\text{guess 1} - \text{guess 2}}{\text{solution 1} - \text{solution 2}} = \frac{0 - 2}{0 - 2} = 1 \\ \text{guess 3} &= \text{guess 2} + m (\text{target} - \text{solution 2}) = 2 + 1(3-2) = 3 \end{align}\]

then, use this guess:

(38)\[\begin{align} z_1 (0.5) &= z_1 (0) + z_2(0) 0.5 = 1.5 \\ z_2 (0.5) &= z_2 (0) + \left( 4z_1(0) \right) 0.5 = 3.0 \\ z_1 (1.0) &= z_1 (0.5) + z_2(0.5) 0.5 = 3.0 \leftarrow \text{solution 3} \\ z_2 (1.0) &= z_2 (0.5) + \left( 4z_1(0.5) \right) 0.5 = 6.0 \end{align}\]

so for solution 3: \(y(1) = 3\) which is the target.

So our answer is \(y'(0) = 3\).