Contents

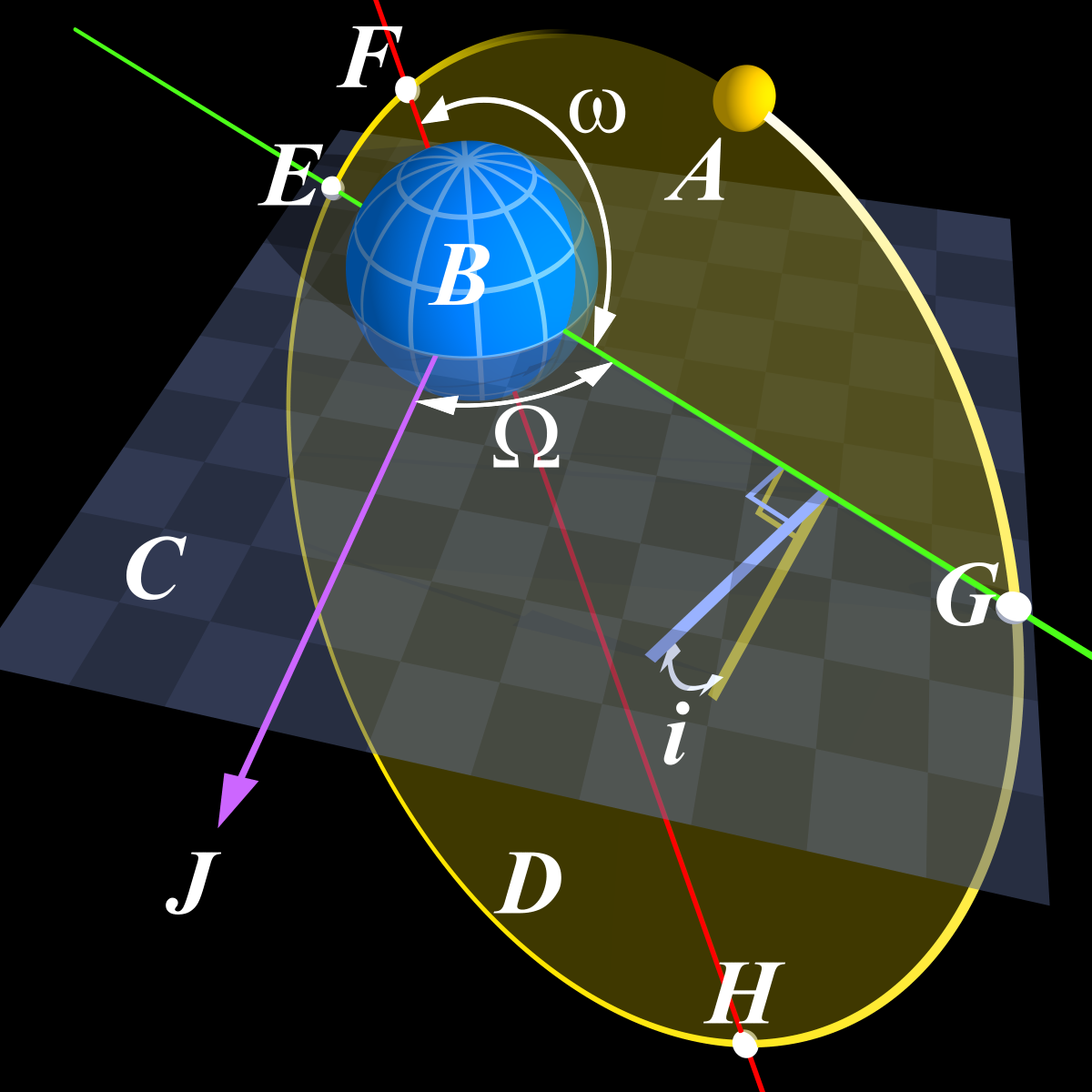
Rendezvous

Rendezvous problems involve the relative position, velocity, and acceleration of two objects in orbit around another (large) body—for example, two spacecraft in orbit around Earth.

import numpy as np
%matplotlib inline
from matplotlib import pyplot as plt

Relative coordinate system

Given two spacecraft A and B, where we know the position and velocity vectors at an instant in time (potentially via their orbital elements), we can determine the relative position, vector, and acceleration of B from the local coordinate system of A.

The problem: given \(\vec{R}_A\), \(\vec{R}_B\), \(\vec{V}_A\), and \(\vec{V}_B\), find \(\vec{r}_{\text{rel}}\), \(\vec{v}_{\text{rel}}\), and \(\vec{a}_{\text{rel}}\) of B with respect to A.

First, determine the relative vectors of B with respect to A in the geocentric equatorial frame:

\[\begin{split} \begin{align} \vec{R}_{B/A} = \vec{R}_{\text{rel}} &= \vec{R}_B - \vec{R}_A \\ \vec{V}_{\text{rel}} &= \vec{V}_B - \vec{V}_A - \vec{\Omega} \times \vec{R}_{\text{rel}} \\ \vec{A}_{\text{rel}} &= \vec{A}_B - \vec{A}_A - \vec{\dot{\Omega}} \times \vec{R}_{\text{rel}} - \vec{\Omega} \times \vec{\Omega} \times \vec{R}_{\text{rel}} - 2 \vec{\Omega} \times \vec{V}_{\text{rel}} \;, \end{align} \end{split}\]

where

\[\begin{split} \begin{align} \vec{A}_A &= -\frac{\mu}{R_A^3} \vec{R}_A \\ \vec{A}_B &= -\frac{\mu}{R_B^3} \vec{R}_B \;. \end{align} \end{split}\]

We need the angular velocity \(\Omega\) and angular acceleration \(\dot{\Omega}\) associated with the moving coordinate system of spacecraft A, where \(\vec{V}_A = \vec{\Omega} \times \vec{R}_A\), and we can determine the angular momentum

\[ \vec{h}_A = \vec{R}_A \times \left( \vec{\Omega} \times \vec{R}_A \right) \;. \]

Then,

\[\begin{split} \begin{align} \vec{\Omega} &= \frac{\vec{h}_A}{R_A^2} = \frac{\vec{R}_A \times \vec{V}_A}{R_A^2} \\ \vec{\dot{\Omega}} &= \frac{d}{dt} \vec{\Omega} = \frac{-2 \vec{\Omega}}{R_A^2} \vec{V}_A \cdot \vec{R}_A \end{align} \end{split}\]

These vectors give us the relative position, velocity, and acceleration in the geocentric equatorial frame, but we would like them in the local coordinate frame of spacecraft A. In other words, where is spacecraft B and how fast is it moving, from the perspective of spacecraft A?

First, define the local coordinate system of spacecraft A:

\[\begin{split} \begin{align} \hat{i} &= \frac{\vec{R}_A}{R_A} \\ \hat{k} &= \frac{\vec{h}_A}{h_A} \\ \hat{j} &= \hat{k} \times \hat{i} \end{align} \end{split}\]

We can write these unit direction vectors with respect to the geocentric equatorial frame:

\[\begin{split} \begin{align} \hat{i} &= L_x \hat{I} + M_x \hat{J} + N_x \hat{K} \\ \hat{j} &= L_y \hat{I} + M_y \hat{J} + N_y \hat{K} \\ \hat{k} &= L_z \hat{I} + M_z \hat{J} + N_z \hat{K} \;, \end{align} \end{split}\]

where \(L_x\) is the first element of \(\hat{i}\), and so on.

The rotation matrix for converting from the local coordinate system to the geocentric equatorial frame is

\[\begin{split} [Q_{xX}] = \begin{bmatrix} L_x & M_x & N_x \\ L_y & M_y & N_y \\ L_z & M_z & N_z \end{bmatrix} \end{split}\]

Then, we can determine the relative vectors from the local coordinate system of A:

\[\begin{split} \begin{align} \vec{r}_{\text{rel}} &= [Q_{xX}]^{\intercal} \vec{R}_{\text{rel}} \\ \vec{v}_{\text{rel}} &= [Q_{xX}]^{\intercal} \vec{V}_{\text{rel}} \\ \vec{a}_{\text{rel}} &= [Q_{xX}]^{\intercal} \vec{A}_{\text{rel}} \end{align} \end{split}\]

Linear orbit theory

We may also want to know how close or far apart two objects are as a function of time. For example, if the Space Shuttle releases a satellite with some initial relative velocity, how far away is it after some time?

We can answer this using linear orbit theory. First, define the position of the object B relative to that of object A: \(\vec{r} = \vec{R} + \vec{\delta}_r\), where \(\vec{\delta}_r\) is relatively small (compared to orbital distances), and insert this into the equation of motion:

\[ \vec{\ddot{R}} + \vec{\ddot{\delta}_r} = \frac{\mu}{r^3} \left( \vec{R} + \vec{\delta}_r \right) \;, \]

where we can express the position of the second object in the denominator using a binomial expansion:

\[ r^{-3} = \left(r^2 \right)^{-3/2} \approx R^{-3} \left[ \frac{-2 R \delta_r}{R^2} \right]^{-3/2} \;. \]

Then, based on the assumptions that \(\vec{R} = R \hat{i}\) and that the orbit of object A is circular, we can solve for the relative position vector of object B as a function of time using the Chlohessy-Wiltshire equations (i.e., modified Hill’s equations):

\[\begin{split} \begin{align} \ddot{\delta_x} - 3 n^2 \delta_x - 2 n \dot{\delta_y} &= 0 \\ \ddot{\delta_y} + 2 n \dot{\delta_x} &= 0 \\ \ddot{\delta_z} + n^2 \delta_z &= 0 \;, \end{align} \end{split}\]

where \(n = \sqrt{\mu / R^3}\) is the mean motion. To solve for the relative position vector as a function of time, we can decompose this into a system of six first-order ODEs, and integrate in time. The initial conditions would be that at \(t = 0\), the initial position components are zero (\(\delta_x, \delta_y, \delta_z = 0\)), and the initial velocity components \(\dot{\delta}_x\), \(\dot{\delta}_y\), and \(\dot{\delta}_z\) are given.

After some time, the distance of object B from A would then be \(\delta_r = \sqrt{\delta_x^2 + \delta_y^2 + \delta_z^2}\).

Cowell’s method

We may also want to keep track of the original orbit along with the new orbit, both in the case of a rendezvous problem but also when analyzing orbital perturbations. Cowell’s method allows us to track/integrate the original Kepler orbit, along with the perturbed orbit (i.e., the oscultating orbit) of either the original vehicle or an ejected object.

First, define the position of the object in the perturbed orbit: \(\vec{r} = \vec{\rho} + \vec{\delta}_r\), where \(\vec{\rho}\) is the position in the original Kepler orbit. Then, we can write equations of motion for both orbits:

\[\begin{split} \begin{align} \vec{\ddot{\rho}} + \frac{\mu}{\rho^3} \vec{\rho} &= 0 \\ \vec{\ddot{\delta}}_r + \frac{\mu}{\delta_r^3} \vec{\delta}_r &= \vec{a}_p \;, \end{align} \end{split}\]

where \(\vec{a}_p\) is the acceleration of a perturbing force. In the case of thrust, this is

\[ \vec{a}_p = \frac{T \dot{\delta}_r}{ \delta_r m} \;, \]

but this term can also include other perturbations such as atmospheric drag.

Encke formulation

\[\begin{split} \begin{align} \vec{\ddot{\delta}}_r &= \frac{\mu}{\rho^3} \left( F \vec{r} - \vec{\delta}_r \right) + \frac{T \vec{v}}{v m} \\ \vec{\ddot{\rho}} &= -\frac{\mu}{\rho^3} \vec{\rho} \\ \dot{m} &= -\frac{T}{I_{\text{sp}} g_0} \;, \end{align} \end{split}\]

where

\[\begin{split} \begin{align} \phi &= \frac{-(\delta_x \rho_x + \delta_y \rho_y + \delta_z \rho_z )}{\rho^2} \\ F &= 1 - (1 - 2 \phi)^{-3/2} \\ \vec{v} &= \vec{\dot{\delta}}_r + \vec{\dot{\rho}} \\ \vec{r} &= \vec{\delta}_r + \vec{\rho} \;. \end{align} \end{split}\]

In three dimensions, this problem requires the integration of 13 first-order ODEs in time for 13 variables, all of which need initial conditions.

For example, if we are looking for the new perturbed orbit after some engine burn for some time, then the initial relative position and velocity components would be zero: \(\delta_x, \delta_y, \delta_z, \dot{\delta}_x, \dot{\delta}_y, \dot{\delta}_z = 0\), the initial position and velocity vectors of the Kepler orbit would be based on the state vector where the burn starts (\(\rho_x, \rho_y, \rho_z, \dot{\rho}_x, \dot{\rho}_y, \dot{\rho}_z\)), and the initial mass is the starting mass of the vehicle (\(m = m_0\)).

After some integrating for some time, we can determine the new position and velocity:

\[\begin{split} \begin{align} \vec{R} &= \left[ \rho_x + \delta_x , \rho_y + \delta_y, \rho_z + \delta_z \right] \\ \vec{V} &= \left[ \dot{\rho}_x + \dot{\delta}_x , \dot{\rho}_y + \dot{\delta}_y, \dot{\rho}_z + \dot{\delta}_z \right] \;. \end{align} \end{split}\]
Orbit transfers Orbit Perturbations