Contents

Orbits in space

Now that we know how to describe orbits in the perifocal frame, we need will look at how to move from this frame of reference to a more-general location in space.

This module will cover:

  • Geocentric equatorial frame

  • Orbital elements

  • Gibbs problem

  • Gauss problem/Lambert theorem

  • Topocentric frame

import numpy as np
%matplotlib inline
from matplotlib import pyplot as plt

Geocentric equatorial frame

In the geocentric equatorial frame, the Earth lies at the center and spins, where the \(X-Y\) plane aligns with the equatorial plane of the planet and the planet’s axis of rotation points in the \(Z\) direction of the frame.

Note that this frame does not align with the plane of the ecliptic (the solar plane), since the Earth’s axis is tilted 23.44°.

Depiction of geocentric equatorial frame

Fig. 6 Diagram of geocentric equatorial frame. Original source by Tfr000, shared under CC BY-SA

The \(X\) axis of the geocentric equatorial frame always points in the same direction, towards the vernal equinox. This direction is also referred to as the first point in Aries, or with ♈, since this pointed to the constellation Aries back when the Greeks came up with the idea. However, due to the precession of the Earth’s tilt, the direction changes over time, and it now points towards Pisces. In the year 2600, the vernal equinox will point towards Aquarius.

Due to this precession, for precise orbital determinations we need to specify the direction of \(X\) via the appropriate 50-year epoch. We are currently in the 2000 epoch, but in 2025 we will pass into the 2050 epoch.

For an object in space, we can specify its position in the geocentric equatorial frame via its distance from the center (\(r\)), the angle away from the \(X\) direction in the equatorial plane is the right ascension (\(\alpha\)), and the angle above the plane is the declination (\(\delta\)).

Orbital elements

In the perifocal frame, we can specify an object in orbit using the eccentricity \(e\), the specific angular momentum \(h\), and the true anomaly \(\theta\). To specify the orientation of this plane in the geocentric equatorial frame, we need three additional quantities.

Diagram with classical orbital elements

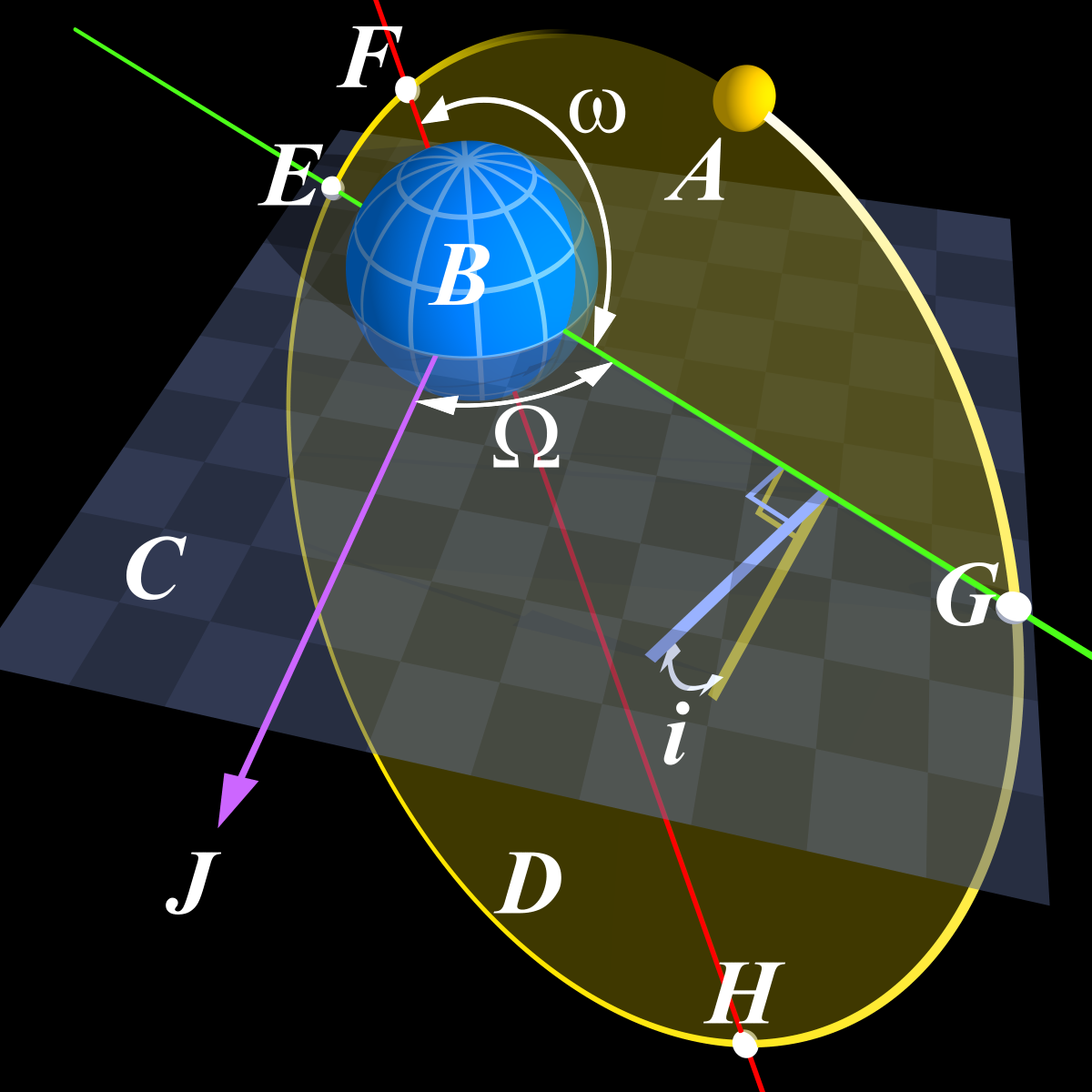
Fig. 7 Diagram showing the orbital elements. Note that this uses \(\nu\) for true anomaly, while we usually use \(\theta\) here. Source: Lasunncty at the English Wikipedia / CC BY-SA

The additional three quantities needed are the:

  • right ascension \(\Omega\), which is the angle between the reference direction \(\vec{X}\), or ♈, and the direction of the line of the ascending node \(\vec{N}\);

  • inclination \(i\), the angle of the perifocal frame away from the reference plane; and

  • argument of periapse/perigee \(\omega\), the angle between the line of ascending node and direction of periapse \(\vec{e}\).

The orbit is prograde if \(i <\) 90°, and retrograde if \(i >\) 90°.

Now, we have the six orbital elements needed to uniquely specify an orbit in a two-body system: \(h, e, \theta, \Omega, i, \omega\).

Two-line element sets

Two-line element (TLE) sets, or “elsets”, are a standard format used to encode and distribute the oribital elements of an object in space, along with other important information. These were originally designed for a 72-column punchcard format, like what FORTRAN 77 used.

Particular column ranges encode specific information and quantities. Here is an example for the NOAA-6 satellite.

NOAA 6
1 11416U 84123  A 86 50.28438588 0.00000140  00000-0  67960-4 0  5293
2 11416  98.5105  69.3305 0012788  63.2828 296.9658 14.24899292346978

Line 0 contains the satellite name (up to 24 characters). On line 1: by column range:

Column

Description

01

line number (1)

03-07

satellite number designated by USSPACECOM (11416)

08

classification (U means unclassified)

10-11

international designator, launch year (84 means 1984)

12-14

international designator, launch number (123 means 124th launch)

15-17

international designator, piece (A means first object)

19-20

Epoch year (86 means 1986)

21-32

Epoch, Julian day fraction (50.28438588 converts to 050:06:49:30.94)

34-43

ballistic coefficient, or 1st time derivative of mean motion (0.00000140)

45-52

2nd derivative of mean motion, usually blank (00000-0 = 0.00000)

54-61

BSTAR, or drag term (67960-4 means 0.67960e-4)

63

ephemeris type (0)

65-69

element number and checksum

On line 2:

Column

Description

01

line number (2)

03-07

satellite number designated by USSPACECOM (11416)

09-16

inclination in degrees (98.5105 means 98.5105°)

18-25

right ascension of the ascending node in degrees (69.3305 means 69.3305°)

27-33

eccentricity (0012788 means 0.0012788)

35-42

argument of perigee, in degrees (63.2828 means 63.2828°)

44-51

mean anomaly, in degrees (296.9658 means 296.9658°)

53-63

mean motion, orbits per day (14.24899292)

64-68

revolution number at epoch, in orbits (34697)

69

checksum

Calculating orbital elements from state vectors

Given the state vectors \(\vec{r}\) and \(\vec{v}\), a typical problem is to calculate the six orbital elements.

First, calculate the magnitudes of relevant vectors:

\[ r = | \vec{r} | \quad v = |\vec{v}| \quad v_r = \frac{\vec{r} \cdot \vec{v}}{r} \]

Then, calculate each of the orbital elements:

  1. Specific angular momentum:

    \[ \vec{h} = \vec{r} \times \vec{v} \quad h = |\vec{h}| \]

  2. Inclination:

    \[ i = \cos^{-1} \left( \frac{h_z}{h} \right) \]

  3. Right ascension of the ascending node:

    \[\begin{split} \begin{align} \vec{N} &= \vec{K} \times \vec{h} \\ N &= \left| \vec{N} \right| \\ \Omega &= \begin{cases} \cos^{-1} \left( \frac{N_x}{N} \right) \quad \text{if } N_Y \geq 0 \;, \\ 360° - \cos^{-1} \left( \frac{N_x}{N} \right) \quad \text{if } N_Y < 0 \;, \\ \end{cases} \end{align} \end{split}\]

  4. Eccentricity:

    \[ \vec{e} = \frac{1}{\mu} \left[ \left( v^2 - \frac{\mu}{r} \right) \vec{r} - r v_r \vec{v} \right] \quad e = | \vec{e} | \]

  5. Argument of perigee (i.e., argument of periapse):

    \[\begin{split} \omega = \begin{cases} \cos^{-1} \left( \frac{\vec{N} \cdot \vec{e}}{N e} \right) \quad \text{if } e_Z \geq 0 \;, \\ 360° - \cos^{-1} \left( \frac{\vec{N} \cdot \vec{e}}{N e} \right) \quad \text{if } e_Z < 0 \;, \\ \end{cases} \end{split}\]

  6. True anomaly:

    \[\begin{split} \theta = \begin{cases} \cos^{-1} \left( \frac{\vec{e} \cdot \vec{r}}{e r} \right) \quad \text{if } v_r \geq 0 \;, \\ 360° - \cos^{-1} \left( \frac{\vec{e} \cdot \vec{r}}{e r} \right) \quad \text{if } v_r < 0 \;, \\ \end{cases} \end{split}\]

Calculating state vectors from orbital elements

The opposite from above is calculating the position and velocity state vectors from the six orbital elements. We can do this by using \(h, e, \theta\) to determine \(\vec{r}\) and \(\vec{v}\) in the perifocal frame, and then rotating into the geocentric equatorial frame of reference (\(\vec{R}\) and \(\vec{V}\)).

We can find the overall transformation by combining three rotation matrices:

  1. Yaw about the \(Z\) axis:

    \[\begin{split} R_3 \left( \Omega \right) = \begin{bmatrix} \cos \Omega & \sin \Omega & 0 \\ -\sin \Omega & \cos \Omega & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{split}\]

  2. Pitch about the \(X_P^{\prime}\) axis:

    \[\begin{split} R_1 \left( i \right) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos i & \sin i \\ 0 & -\sin i & \cos i \end{bmatrix} \end{split}\]

  3. Roll about the \(Z_P^{\prime}\) axis:

    \[\begin{split} R_3 \left( \omega \right) = \begin{bmatrix} \cos \omega & \sin \omega & 0 \\ -\sin \omega & \cos \omega & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{split}\]

  4. Calculate the total transformation matrix:

    \[ \left[ Q_{Xx} \right] = R_3 \left( \omega \right) R_1 (i) R_3 \left( \Omega \right) \;, \]

    which involves matrix multiplications.

  5. Calculate the new position and velocity vectors in the geocentric equatorial frame:

    \[\begin{split} \begin{align} \vec{R} &= \left[ Q_{Xx} \right]^{\top} \vec{r} \\ \vec{V} &= \left[ Q_{Xx} \right]^{\top} \vec{v} \;, \end{align} \end{split}\]

    where \(\vec{r}\) and \(\vec{v}\) are the state vectors in the perifocal frame:

    \[\begin{split} \begin{align} \vec{r} &= \frac{h^2 / \mu}{1 + e \cos \theta} \begin{bmatrix} \cos \theta & \sin \theta & 0 \end{bmatrix} \\ \vec{v} &= \frac{\mu}{h} \begin{bmatrix} -\sin \theta & e + \cos \theta & 0 \end{bmatrix} \end{align} \end{split}\]

Gibbs problem

One possible situation is determining the orbit from three sightings / position vectors; this is the Gibbs problem.

The problem: Given \(\vec{R}_1, \vec{R}_2, \vec{R}_3\), find the six orbital elements \(h, e, \theta, \omega, \Omega, i\).

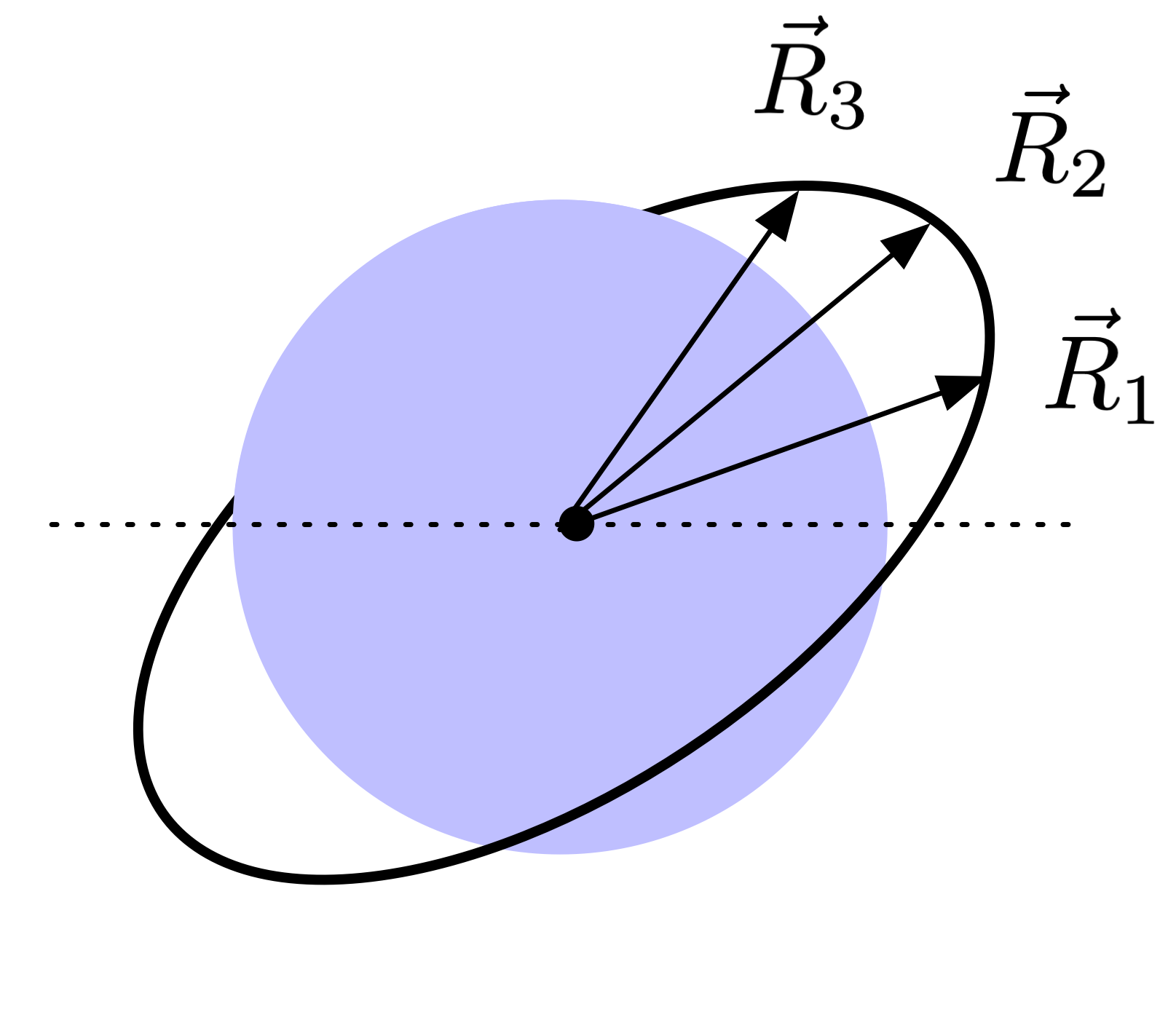
Diagram showing Gibbs problem

Fig. 8 Diagram showing Gibbs problem.

Note that the three position vectors must lie in the same plane, otherwise a stable two-body orbit is not possible.

The goal here is to calculate the velocity vector at location 1, and then with \(\vec{R}_1\) and \(\vec{V}_1\) the orbital elements can be found using the steps given above:

\[ \vec{V}_1 = \sqrt{ \frac{\mu}{N D} } \left( \frac{\vec{D} \times \vec{R}_1}{r_1} + \vec{S} \right) \;, \]

where the magnitudes of the position vectors are \(r_1 = \left| \vec{R}_1 \right|\), \(r_2 = \left| \vec{R}_2 \right|\), \(r_3 = \left| \vec{R}_3 \right|\), and the other vectors are

\[\begin{split} \begin{align} \vec{N} &= r_1 \left( \vec{R}_2 \times \vec{R}_3 \right) + r_2 \left( \vec{R}_3 \times \vec{R}_1 \right) + r_3 \left( \vec{R}_1 \times \vec{R}_2 \right) \\ \vec{D} &= \vec{R}_2 \times \vec{R}_3 + \vec{R}_3 \times \vec{R}_1 + \vec{R}_1 \times \vec{R}_2 \\ \vec{S} &= \vec{R}_1 (r_2 - r_3) + \vec{R}_2 (r_3 - r_1) + \vec{R}_3 (r_1 - r_2) \;, \end{align} \end{split}\]

and the magnitudes are \(N = \left| \vec{N} \right|\) and \(D = \left| \vec{D} \right|\).

Warning

You need to check that \(\vec{D} \neq 0\), \(\vec{N} \neq 0\), and that \(\vec{D} \cdot \vec{N} \geq 0\).

Lambert’s problem

Another fundamental problem is Lambert’s problem, which is finding the orbit that connects two points in space for a given transfer time.

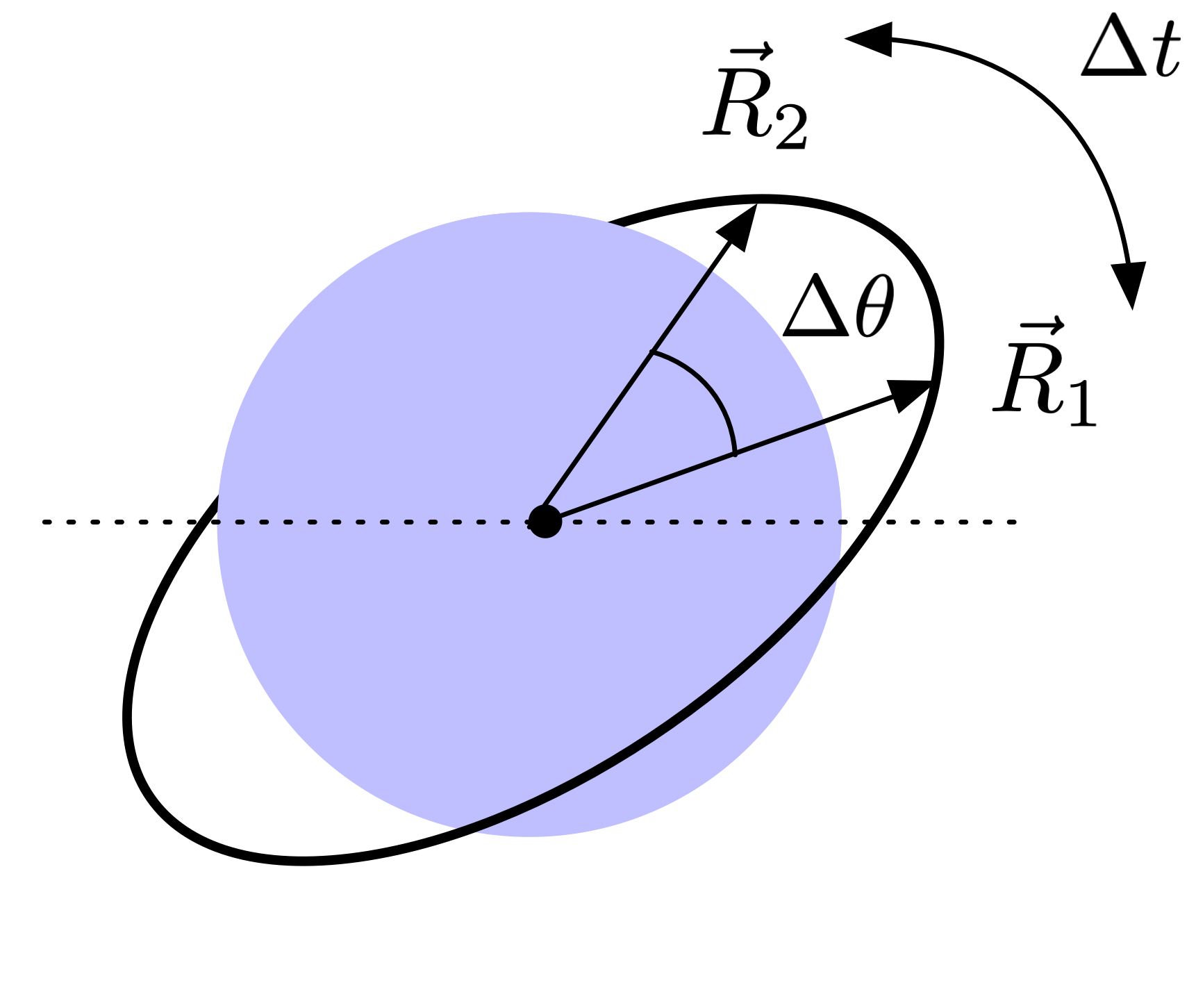
Diagram showing Lambert problem

Fig. 9 Diagram showing Lambert’s problem of orbital transfer between two points.

Problem: Given \(\vec{R}_1\), \(\vec{R}_2\), and \(\Delta t\), find the six orbital elements.

Solution steps:

  1. Calculate the radial position magnitudes: \(r_1 = \left| \vec{R}_1 \right|\) and \(r_2 = \left| \vec{R}_2 \right|\).

  2. Calculate the change in true anomaly, depending on if the orbit is prograde or retrograde (assume prograde to start):

    \[\begin{split} \begin{align} \text{if prograde } (i < 90°): \Delta \theta &= \begin{cases} \cos^{-1} \left( \frac{\vec{R}_1 \cdot \vec{R}_2}{r_1 r_2} \right) \quad \text{if } \left(\vec{R}_1 \times \vec{R}_2 \right)_Z \geq 0 \\ 360° - \cos^{-1} \left( \frac{\vec{R}_1 \cdot \vec{R}_2}{r_1 r_2} \right) \quad \text{if } \left(\vec{R}_1 \times \vec{R}_2 \right)_Z < 0 \end{cases} \\ \text{if retrograde } (i > 90°): \Delta \theta &= \begin{cases} \cos^{-1} \left( \frac{\vec{R}_1 \cdot \vec{R}_2}{r_1 r_2} \right) \quad \text{if } \left(\vec{R}_1 \times \vec{R}_2 \right)_Z < 0 \\ 360° - \cos^{-1} \left( \frac{\vec{R}_1 \cdot \vec{R}_2}{r_1 r_2} \right) \quad \text{if } \left(\vec{R}_1 \times \vec{R}_2 \right)_Z \geq 0 \end{cases} \\ \end{align} \end{split}\]

  3. Calculate the quantity \(A\):

    \[ A = \sin \Delta \theta \sqrt{ \frac{r_1 r_2}{1 - \cos \Delta \theta}} \]

  4. Iteratively solve for the universal anomaly parameter \(z\):

    \[\begin{split} \begin{align} y(z) &= r_1 + r_2 + A \frac{z S(z) - 1}{\sqrt{C(z)}} \\ \sqrt{\mu} \, \Delta t &= \left[ \frac{y(z)}{C(z)}\right]^{3/2} S(z) + A \sqrt{y(z)} \end{align} \end{split}\]

    A reasonable initial guess is \(z=1\). Then, these equations can be used with an equation solver like fzero in Matlab or scipy.optimize.root_scalar in Python to solve for \(z\). If \(z < 0\), the orbit is hyperbolic, and if \(z > 0\) the solution is elliptic.

  5. Calculate the universal Lagrange coefficients using the value of \(z\):

    \[\begin{split} \begin{align} f &= 1 - \frac{y(z)}{r_1} \\ g &= A \sqrt{ \frac{y(z)}{\mu} } \\ \dot{f} &= \frac{\sqrt{\mu}}{r_1 r_2} \sqrt{ \frac{y(z)}{C(z)}} \left[ z S(z) - 1 \right] \\ \dot{g} &= 1 - \frac{y(z)}{r_2} \end{align} \end{split}\]

    where \(C(z)\) and \(S(z)\) are the Stumpf functions.

  6. Calculate the velocities at each position:

    \[\begin{split} \begin{align} \vec{V}_1 &= \frac{1}{g} \left( \vec{R}_2 - f \vec{R}_1 \right) \\ \vec{V}_2 &= \frac{1}{g} \left( \dot{g} \vec{R}_2 - \vec{R}_1 \right) \\ \end{align} \end{split}\]

  7. With either state vector combination (say, \(\vec{R}_1\) and \(\vec{V}_1\)), you can now obtain the orbital elements.

If you find that the orbit is actually retrograde (\(i > 90°\)), then repeat the process starting at step 2 using the appropriate equation.

Topocentric frame

The topocentric frame describes the location of an orbiting object from a viewing location on the Earth’s surface, based on instantaneous geodetic latitude (\(\phi\)) and longitude (\(\theta\)). This will be an instantaneous relationship, since latitude and longitude are fixed but on the rotating surface of the Earth.

The problem: find the range and elevation from a viewing point on the surface, given the instantaneous position vector of the orbiting object in the geocentric equatorial frame \(\vec{R}_{X}\), the geodetic latitude \(\phi\), and the geodetic longitude \(\theta\).

Subscript meanings:

  • capital \(X\): vector in the geocentric equatorial frame

  • lowercase \(x\): vector in the topocentric frame

The solution is to find the relative position vector in the geocentric equatorial frame, then rotate that into the local topocentric frame:

\[\begin{split} \begin{align} \vec{\rho}_X &= \vec{R}_X - \vec{R}_{\text{site}} \\ \vec{\rho}_x &= [Q_{Xx}] \vec{\rho}_X \;, \end{align} \end{split}\]

where \(\vec{R}_{\text{site}}\) is the position vector from the Earth’s center (i.e., the origin of the geocentric equatorial frame):

\[\begin{split} \vec{R}_{\text{site}} = \left[ \frac{\bar{R}_e}{\sqrt{1 - (2f - f^2) \sin^2 \phi}} + H \right] \cos \phi \left\{ \cos \theta \, \vec{I} + \sin \theta \, \vec{J} \right\} + \\ \left[ \frac{\bar{R}_e (1 - f)^2}{\sqrt{1 - (2f - f^2) \sin^2 \phi}} + H \right] \sin \phi \, \vec{K} \;, \end{split}\]

where \(\bar{R}_e\) = 6378 km is the average radius of the Earth, \(H\) is the altitude/elevation of the observing site, and \(f = 0.003353\) is the oblatedness of the Earth. Then, \([Q_{Xx}] = R_1 \left( \phi \right) \cdot R_3 \left( \theta \right)\) is the rotation matrix:

\[\begin{split} \begin{align} R_1 \left( \phi \right) &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & -\sin \phi & \cos \phi \\ 0 & \cos \phi & \sin \phi \end{bmatrix} \\ R_3 \left( \theta \right) &= \begin{bmatrix} -\sin \theta & \cos \theta & 0 \\ \cos \theta & \sin \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \;. \end{align} \end{split}\]

Then, we can find the range with \(\left| \vec{\rho}_x \right|\) and elevation with

\[ a = \sin^{-1} \left( \hat{\rho}_z \right) \quad \hat{\rho} = \frac{\vec{\rho}_x}{\left| \vec{\rho}_x \right|} \;, \]

where \(\hat{\rho}_z\) is the \(z\)-component of the unit position vector \(\hat{\rho}\).

Two-body problems Orbit transfers